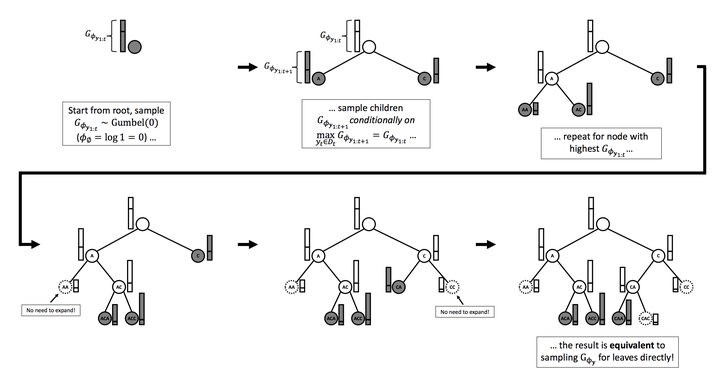
Ancestral Gumbel-Top-k sampling
Abstract
We develop ancestral Gumbel-Top-k sampling: a generic and efficient method for sampling without replacement from discrete-valued Bayesian networks, which includes multivariate discrete distributions, Markov chains and sequence models. The method uses an extension of the Gumbel-Max trick to sample without replacement by finding the top k of perturbed log-probabilities among all possible configurations of a Bayesian network. Despite the exponentially large domain, the algorithm has a complexity linear in the number of variables and sample size k. Our algorithm allows to set the number of parallel processors m, to trade off the number of iterations versus the total cost (iterations times m) of running the algorithm. For m=1 the algorithm has minimum total cost, whereas for m=k the number of iterations is minimized, and the resulting algorithm is known as Stochastic Beam Search. We provide extensions of the algorithm and discuss a number of related algorithms. We analyze the properties of Gumbel-Top-k sampling and compare against alternatives on randomly generated Bayesian networks with different levels of connectivity. In the context of (deep) sequence models, we show its use as a method to generate diverse but high-quality translations and statistical estimates of translation quality and entropy.